Estudaremos o comportamento de uma onda se propagando numa corda. Todas as ondas mecânicas precisam de um meio para se propagar. E nesse breve comentário estudaremos as relações que existem para determinarmos a velocidade dessa onda com base na tensão e na densidade de massa do meio em que está se propagando.
Note que para um pulso de onda numa corda, o meio é a corda. No caso de uma onda sonora, o meio é o onde está se propagando o som. Por exemplo, um som de uma sirene de ambulância se propaga no ar, logo o ar é o meio de propagação da sirene. Mas o grito de uma baleia se propaga na água do mar, logo a água do mar é o meio de propagação do grito da baleia.
CARACTERÍSTICAS DO PULSO DE ONDA MECÂNICA E DO MEIO
Se você está caminhando numa calçada pela manhã, e vê uma corrente suspensa por duas barras para fechar um determinado estacionamento particular, você pode observar uma onda e suas caracteristicas. Basta bater levemente sobre a corrente numa das pontas para observar o pulso se propagando numa velocidade até tranquila de acompanhar com os olhos.
Se você passar por outra corrente suspensa, mas agora uma corrente mais grossa e bater com a mesma intensidade na corrente verá que a velocidade da propagação da onda é ainda menor, mais fácil de acompanhar com os olhos.
A relação da velocidade de um pulso de onda numa corda/corrente é obtida por essa expressão:
Velocidade: do pulso de onda
Tensão: da corda (meio de propagação)
Densidade da massa: da corda (meio de propagação)
Tensão: da corda (meio de propagação)
Densidade da massa: da corda (meio de propagação)
Então além da massa (densidade de massa) da corrente, a tensão em que ela está submetida também influencia na velocidade da propagação da onda. Olhando para expressão notamos que a Tensão é diretamente proporcional à velocidade do pulso, ou seja quanto mais esticado estiver a corda, maior será a Tensão submetida, logo a velocidade do pulso também será maior.
Nos livros também encontramos a expressão simplificada:
Usando essas relações você pode certamente encontrar o valor de qualquer das grandezas envolvidas, basta saber o valor das outras duas.

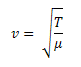
legal
ResponderExcluirem que meio a onda mecânica se propaga com maior velocidade?
ResponderExcluirQual é a máxima velocidade de uma onda mecânica?
ResponderExcluir